一、问题描述
在图算法中,从某点开始,计算到其他点最短的路径是十分常见的问题,而这一问题有许多变种,本文着重于从某点开始到图中所有其他点的最短路径,称为 单源最短路径问题(Single-source Shortest Paths)。
二、特殊情况
负权重的边
在单源最短路径中,负权重的边并非不允许存在,但要求是不存在从源结点可以到达权重为负的环路。因为如果存在可以抵达的权重为负的环路,那么只要不断沿着环路前进,总权重则永远会降低。
环路
显然,在一条最短路径上不可能包含环路,因为之前已经讨论过不可能存在负权重环路,若权重为正,那么只需要将这条环路从路径上去除,得到的权重势必比原来的小。
还有一种环路权重为 0 的情况,无论添加与否并不影响到总权重。为保证问题的一般性,最后结果以没有环路为准,也就是说无论什么情况,最终结果均不含环路。
三、通用操作
首先,为了算法的简单以及路径的表示,对于每个结点都维持两个属性:
v.d:当前从源结点到结点v的最短路径权重v.prev:在最短路径中,结点v的前驱
初始化
1
2
3
4
5
6
7
initialize(V s){
for(v in G.V){
v.d = +∞
v.prev = null
}
s.d = 0
}
将所有结点的最短路径权重设为正无穷,之后在算法中比较就可以使其不断降低。最后石源结点的路径权重设为 0 。
松弛操作
松弛操作(relaxation) 用于更新某个结点的d属性,检查是否可以使权重降低。
1
2
3
4
5
6
relax(V u, V v){
if(v.d > u.d + w(u, v)){
v.d = u.d + w(u, v)
v.prev = u
}
}
传入两个结点,如果 u 的当前权重大于 v 的权重加两个点之间的边权重,说明从 v 走到 u 的这条路径比原来的权重要低,所以更新 u.d 并使 u 的前驱结点设为 v 即可。
四、Bellman-Ford 算法
Bellman-Ford 算法中不要求权重均为非负值,而且会返回一个布尔值以表明是否存在源结点可到达的负权重环路。
算法利用松弛操作来逐渐降低每个点的d,直到达到最低的权重,即期望的最短路径。
1
2
3
4
5
6
7
8
9
10
11
12
bellman_ford(V s){
initialize(s);
for(int i=0; i< |G.V|-1 ; ++i){
for(e in G.E)
relax(e.v1, e.v2)
}
for(e in G.E){
if(e.v1.d > e.v2.d + w(e.v1, e.v2))
return FALSE
}
return TRUE
}
首先进行初始化,之后对所有边进行松弛操作,反复进行 \(\vert G.V \vert -1\) 次(正确性不在此讨论)。此时各节点的路径权重已处理完毕,接下来的循环检查是否存在负权重环路。因为对于不存在的路径,此时已达到最小,而如果存在那么权重可以继续减小,所以检查每条边权重能否减小即可。
算法中初始化需要 \(\theta (V)\),松弛操作用到两重循环,分别进行 \(\vert V \vert -1\) 和 \(\lvert E \rvert\) 次,检查的循环进行 \(\vert E\vert\) 次。所以总运行时间由松弛操作的循环决定,时间为 \(O(VE)\) 。
五、有向无环图中的单源最短路径
如标题所示,这一算法要求有向无环图。因为不成环,所以存在负权重的边也不影响到最短路径的存在。
1
2
3
4
5
6
7
8
DAG_SSSP(V s){
topsort()
initialize(s)
for(v in G.V){ //以拓扑排序的次序
for(u in v.adj)
relax(u, v)
}
}
首先需要进行一次拓扑排序,确定一个线性次序,然后依次对每个点的邻接边进行一次松弛操作。
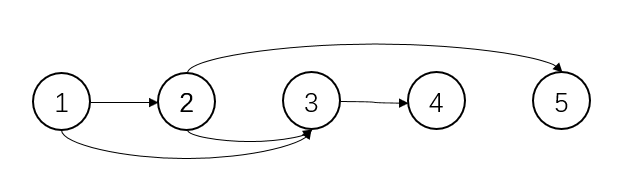
如上图所示,显然如果存在 u 与 v 之间的一条路径,那么 u 必定在 v 左侧。从左到右处理,即按拓扑排序的次序,处理某点时,能够抵达该点的路径必定都被松驰过,则已经是最短路径。
拓扑排序时间复杂度为\(O(V+E)\),初始化需要\(O(V)\),松弛操作对每条边松弛,所以总时间为 \(O(V+E)\)。
六、Dijkstra 算法
Dijkstra 算法能解决有向图上的最短路径问题,但要求所有边权重为非负值。
1
2
3
4
5
6
7
8
9
10
11
dijkstra(V s){
initialize(s)
S = 0 //定义空集
Q = G.V //定义最小优先队列,根据d排序
while(!Q.isEmpty()){
u = Q.pop()
S.add(u)
for(v in u.adj)
relax(u,v)
}
}
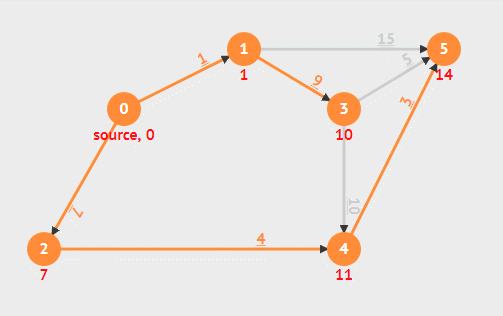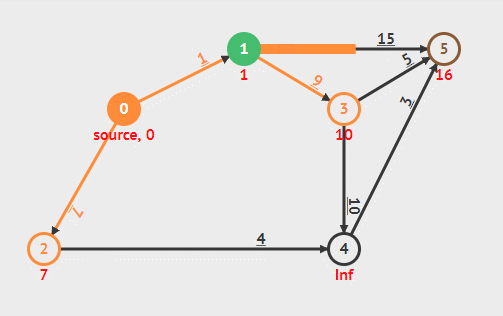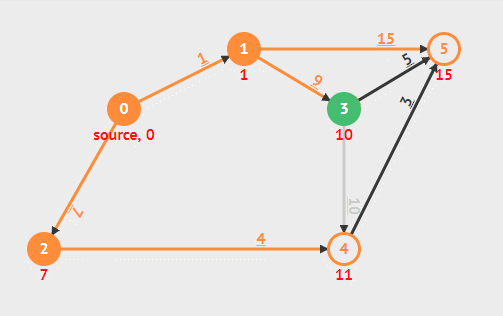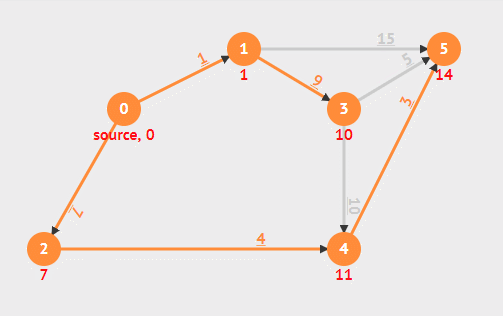
在整个过程中维护一个集合 S ,用于存放已经找到最短路径的结点,还有一个最小优先队列 Q ,每次从中找出最短路径估计最小的,即 Q 中第一个,加入 S ,并对其所有邻接边松弛。
Gif 根据visugo.net 制作