在图的使用中,不可避免的就是对图的搜索,最为基础的就是广度优先搜索(Breadth First Search)和深度优先搜索(Depth First Search)。
广度优先搜索
广度优先搜索,又名宽度优先搜索,从根节点开始,沿着宽度遍历整张图,直到所有节点都被访问过为止。在下图可以清楚的看出这一点。
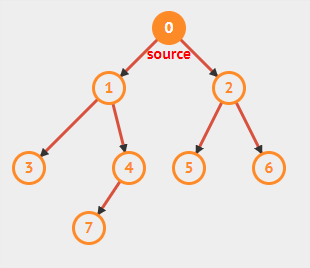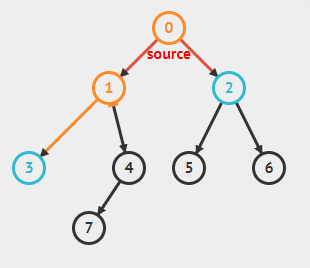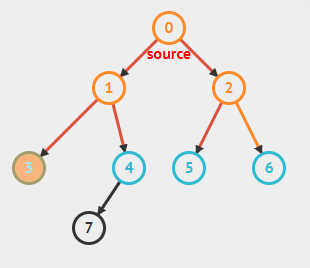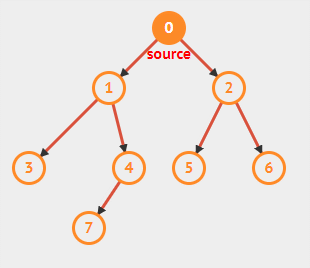
在算法中,每一个结点都被涂上一个颜色,白色、灰色和黑色,白色代表尚未发现,灰色代表被发现但尚未检查,颜色即将改变,黑色代表访问完毕。此外利用一个优先队列记录被发现的但未访问完成的节点,即灰色节点。同时,在搜索同时会生成一颗广度优先树,所以对于每个节点都定义一个属性 \(pi\),用以保存前驱结点。
具体实现方法为:
- 先初始化,将所有结点涂白,并将前驱节点置为 NULL 。
- 先将根节点涂灰,并放入队列中。
- 在队列中取出第一个结点 u ,并检查与其相邻的结点 v 。如果 v 为白,则将其涂灰并设置前驱结点,之后将其置入队列。
- 结点 u 访问完成,将其涂黑。
- 重复步骤 3 ,直到队列为空。
在上图中,蓝色代表灰色结点(被发现,但未检查),黑色代表白色结点(尚未发现),橙色代表黑色结点(已访问完毕)。
实现代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
// 此代码中以邻接矩阵graph的形式来实现
// 所有结点被存储在数组vertex中,并对每个结点标号 0, 1, 2......,总共 v 个结点
// 函数传进参数 s,表示结点编号
void Graph::BFS(int s) {
// 步骤 1
for (int i = 0; i < v; i++) {
vertex[i].color = WHITE;
vertex[i].pi = nullptr;
}
// 步骤 2
vertex[s].color = GRAY;
vertex[s].pi = nullptr;
std::priority_queue<int> Q;
Q.push(s);
while (Q.empty() != true) { //步骤 5 循环
// 步骤 3
int u = Q.top();
Q.pop();
for (int i = 0; i < v; i++) {
if (graph[u][i] != 0) {
if (vertex[i].color == WHITE) {
vertex[i].color = GRAY;
vertex[i].pi = &vertex[u];
Q.push(i);
}
}
}
// 步骤 4
vertex[u].color = BLACK;
}
}
深度优先搜索
深度优先搜索相对于广度优先而言,顾名思义,会优先沿着一条路走到底,之后再回退,再选择其他的路继续。
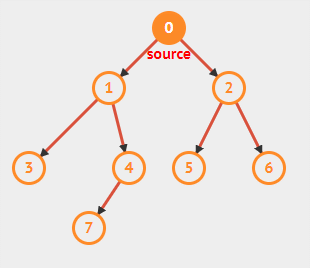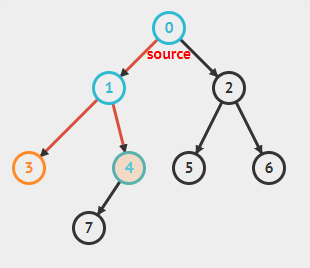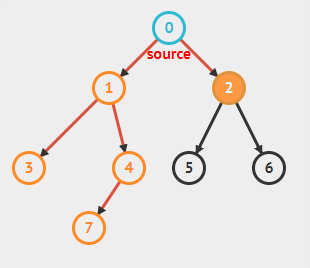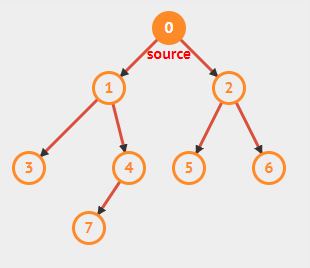
与广度优先搜索相同,会使用黑白灰三色来标记结点,用 \(pi\) 标记前驱结点以实现深度优先树。
具体实现方法中会涉及两个函数 DFS 和 DFS-Visit ,DFS 中负责初始化和对每一个结点进行搜索,DFS-Visit 则对给定结点进行搜索。
DFS 具体做法为:
- 先初始化,将所有节点涂白,并将前驱结点置为 NULL 。
- 对所有结点进行遍历,如果结点为白,则对其进行搜索 DFS-Visit 。
DFS-Visit 要求传进一个结点 u ,具体内容为:
- 将结点 u 涂灰。
- 检查与结点 u 所有相连结点,如果为白,则对其设置前驱结点,再以递归方式对其访问 DFS-Visit 。
- 完成后结点 u 访问完毕,将其涂黑。
颜色含义与广度优先中相同。
具体实现代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
// 此代码中以邻接矩阵graph的形式来实现
// 所有结点被存储在数组vertex中,并对每个结点标号 0, 1, 2......,总共 v 个结点
// 函数传进参数 i,表示结点编号
void Graph::DFS() {
// 步骤 1
for (int i = 0; i < v; i++) {
vertex[i].color = WHITE;
vertex[i].pi = nullptr;
}
// 步骤 2
for (int i = 0; i < v; i++) {
if (vertex[i].color == WHITE) {
DFSVisit(i);
}
}
}
void Graph::DFSVisit(int i) {
// 步骤 1
vertex[i].color = GRAY;
// 步骤 2
for (int j = 0; j < v; j++) {
if (graph[i][j] != 0) {
if (vertex[j].color == WHITE) {
vertex[j].pi = &vertex[i];
DFSVisit(j); // 递归方式继续搜索
}
}
}
// 步骤 3
vertex[i].color = BLACK;
}
简化
从上述代码中可以看出,在检查一个结点是否访问过时,是以是否为白色为根据,所以黑色与灰色结点在实际实现中作用相同,仅帮助理解之用。同时,如果不使用到生成树的形式,\(pi\) 同样可以被省略。
精简后的 DFS :
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// 代码中变量定义与之前相同
// visited用以记录结点是否被访问过
void Graph::DFS_Simplified(int s) {
for (int i = 0; i < v; i++)
visited[i] = 0; // 初始化访问状态
DFSVisit_Simplified(s);
}
void Graph::DFSVisit_Simplified(int i) {
visited[i] = 1;
for (int j = 0; j < v; j++) {
// 如果与结点 i 相连的结点未被访问,则对其访问
if (graph[i][j] != 0 && visited[j] == 0)
DFSVisit_Simplified(j);
}
}
图片和gif根据 visualgo.net 制作