二叉堆,简称堆(Heap),可以被看成近似的完全二叉树,除了最底层外这棵树是充满的。
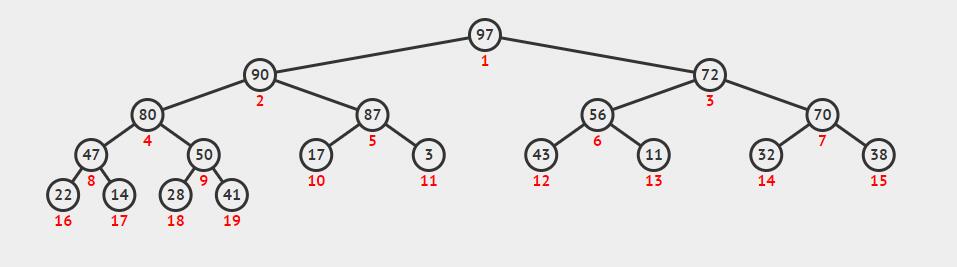
如图所示,从顶层元素开始标号,除了底层外都是充满的。
最大(最小)堆
最大(最小)堆的性质为:对于任何节点,该节点的值必须大(小)于其子节点的值。上图所示即为最大堆。
本文中以最大堆为例。
基本操作&原型
由于堆是一个完全二叉树,如果我们给其编号,那么每一个节点的左右子节点编号都可以很轻易通过计算得到,所以用一个数组来实现并不影响到其性质,却能换来更高的效率。

如上图所示,其为最上面一幅图的数组形式,任何一个节点左节点只需要将编号乘以2,而右节点再加1即可。
然而实际编程中数组下标从0开始,所以在计算子节点时略有区别。
1
2
3
4
5
6
7
8
9
10
11
int left(int i) {
return 2 * i + 1;
}
int right(int i) {
return 2 * i + 2;
}
int parent(int i) {
return (i - 1) / 2 ;
}
另外为了堆可增长,所以采用 vector 来代替数组。下面给出原型:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Heap {
public:
Heap();
Heap(vector<int> vec); //将vec拷贝给heap
int left(int i);
int right(int i);
int parent(int i);
int GetSize();
void MaxHeapify(int i);
void MaxHeapify(int i, int size);
void BuildMaxHeap();
void HeapSort();
void SetVec(vector<int> vec);
int& operator[](int i);
protected:
vector<int> heap;
};
MaxHeapify 维护堆的性质
由于可能在某些操作后,某个节点并不满足最大堆性质,所以我们需要一个函数来维护堆的性质,使该点重新满足最大堆性质。不满足性质则说明该点小于子父节点,那么只需判断该点的值与两个子节点的值大小关系,将最大的与该点交换,如果无需交换则已满足最大堆性质,否则则对交换那一侧子树再进行该操作直至无需交换。这一函数会在之后被频繁使用。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
void Heap::MaxHeapify(int i)
{
size_t l = left(i), r = right(i),max=i;
if (l<heap.size() && heap[l]>heap[max]) {
max = l;
}
if (r<heap.size() && heap[r]>heap[max]) {
max = r;
}
if (max != i) {
swap(heap[i], heap[max]);
MaxHeapify(max);
}
}
在原型中还给出了一个带i和size两个参数的MaxHeapify,具体实现中仅仅使用参数size代替了heap.size(),具体原因会在之后HeapSort中解释。
BuildHeap 建堆
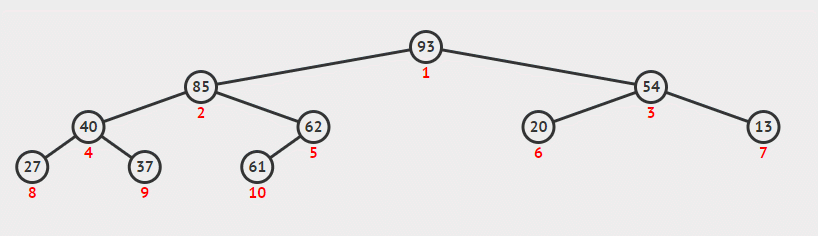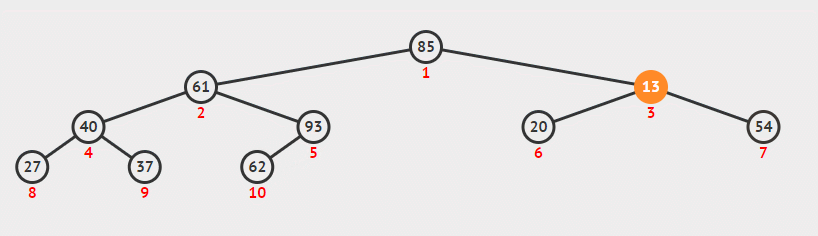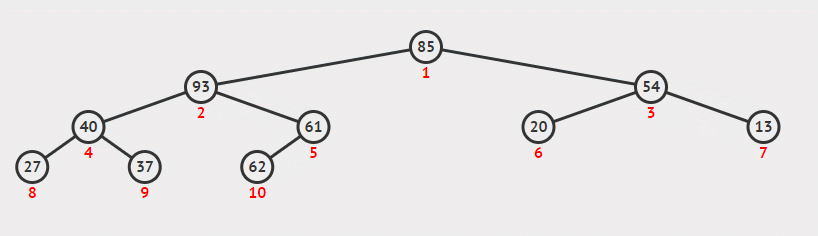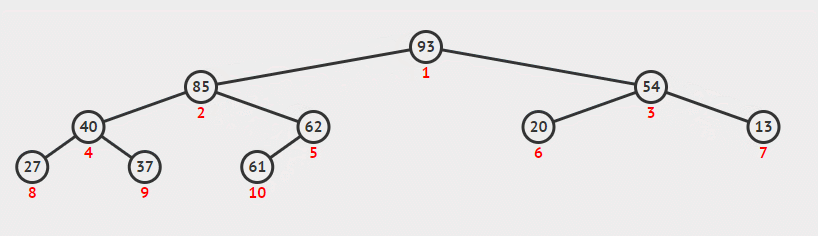
这一函数目的是使一个无序的数组成为最大堆。在之前实现的MaxHeapify可以使某个节点满足最大堆性质,所以我们只需要从底向上依次调用MaxHeapify即可。又因为从n/2+1, …… , n均为叶节点,所以我们只需要从n/2开始。
1
2
3
4
5
6
void Heap::BuildMaxHeap()
{
for (int i = this->GetSize() / 2; i >= 0; i--) {
MaxHeapify(i);
}
}
HeapSort 堆排序
对于二叉堆,每个节点必大于它的子节点,因此根节点必定为整个堆中最大的数字,所以可以十分轻易的得到最大的元素。所以我们每次得到最大的数字后,将其从堆中移出然后维护一次堆的性质又可以得到新堆中最大的元素,按照顺序逆序输出就是排序完的数组。
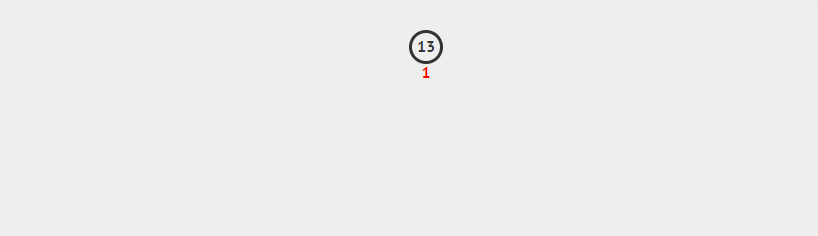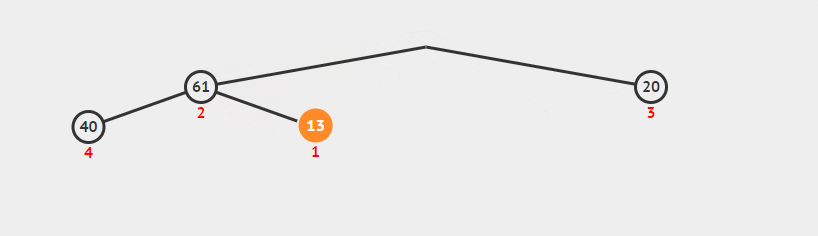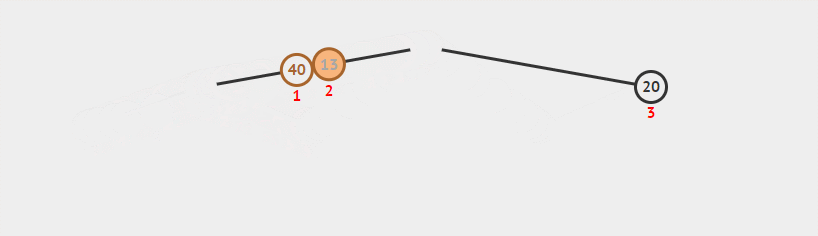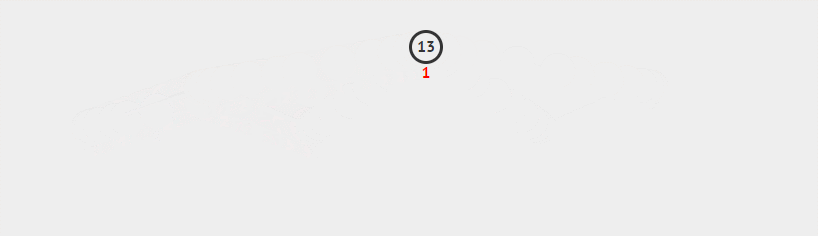
具体实现中,我们将最大的元素放至堆的末尾,与最后一个元素互换,将堆大小减一后再对根节点维护性质,从而得到新堆,不断循环,最后堆就可完成排序。由于之前MaxHeapify中利用heap.size()来得到长度,但在这中我们并未实际改变容器长度,所以就用一个带size参数的MaxHeapify来模拟size的减少。
1
2
3
4
5
6
7
void Heap::HeapSort()
{
for (int i = this->GetSize()-1; i >= 0; i--) {
swap(heap[i], heap[0]);
MaxHeapify(0, i );
}
}
图片和gif根据 visualgo.net 制作