基本概念-树
根据Wiki的定义，树（Tree）是一种抽象数据类型（ADT）或是实作这种抽象数据类型的数据结构，用来模拟具有树状结构性质的数据集合。它是由n（n>=1）个有限节点组成一个具有层次关系的集合。有以下几个特点：
- 每个节点有零个或多个子节点；
- 没有父节点的节点称为根节点；
- 每一个非根节点有且只有一个父节点；
- 除了根节点外，每个子节点可以分为多个不相交的子树；
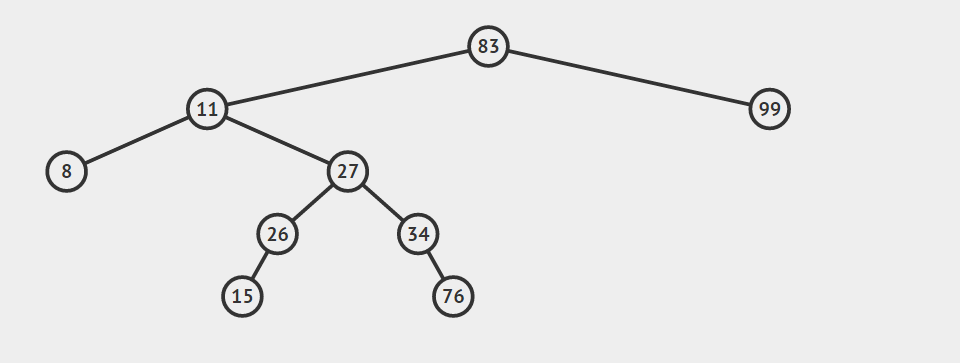
下图即为一棵树，其中83即为根节点，11为8和27的父节点，27和8即为11的子节点。
基本概念-二叉搜索树
二叉搜索树（英语：Binary Search Tree）为树中一种类型，具有以下特点：
- 若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
- 若任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
- 任意节点的左、右子树也分别为二叉查找树；
- 没有键值相等的节点。
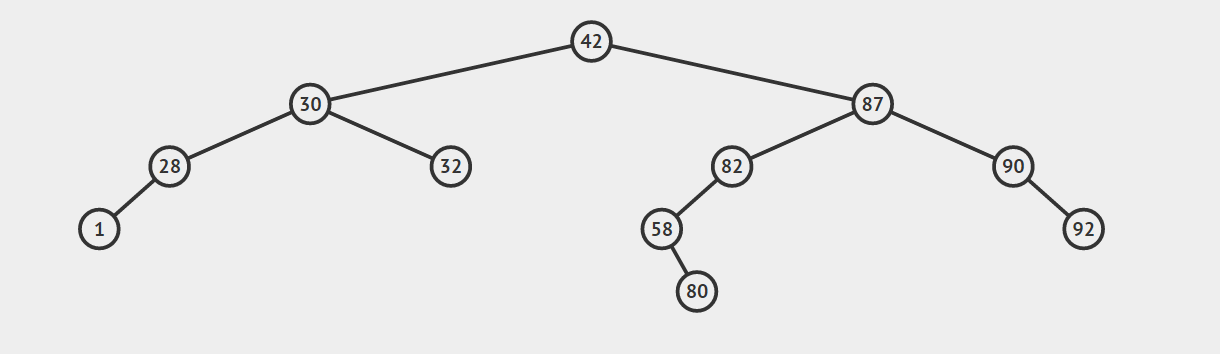
下图即为一颗二叉搜索树，即任何一个节点左边都小于节点值，右边均大于节点值，且不存在重复的节点。
原型声明
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
struct TreeNode;
typedef struct TreeNode *Position;
typedef struct TreeNode *SearchTree;
SearchTree MakeEmpty(SearchTree T);
Position Find(int x, SearchTree T);
Position FindMin(SearchTree T);
Position FindMax(SearchTree T);
SearchTree Insert(int x, SearchTree T);
SearchTree Delete(int x, SearchTree T);
struct TreeNode
{
int data;
TreeNode *Left;
TreeNode *Right;
};
其中定义了树节点的结构，即int型的数据和两个指针分别指向左儿子和右儿子。
这里实现了二叉搜索树的清空、查找、插入和删除功能。
清空
1
2
3
4
5
6
7
8
9
10
SearchTree MakeEmpty(SearchTree T)
{
if (T != NULL) {
MakeEmpty(T->Left);
MakeEmpty(T->Right);
free(T);
T = NULL;
}
return T;
}
即递归的清空每一个树节点释放其内存。
查找
1
2
3
4
5
6
7
8
9
10
11
12
13
Position Find(int x, SearchTree T)
{
if (T == NULL) return NULL;
if (x < T->data) {
return Find(x, T->Left);
}
else if (x>T->data) {
return Find(x, T->Right);
}
else {
return T;
}
}
传入要查找的值和根节点，根据二叉查找树的定义，比某个节点大则去右侧找，同样若比某个节点小则去左边找，然后递归的实现。
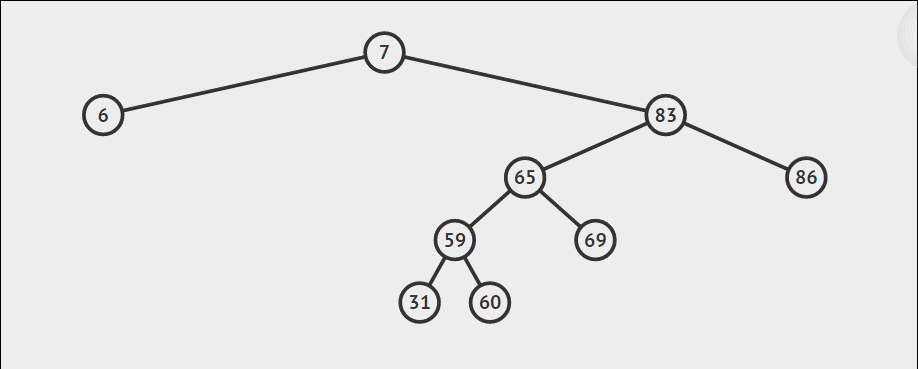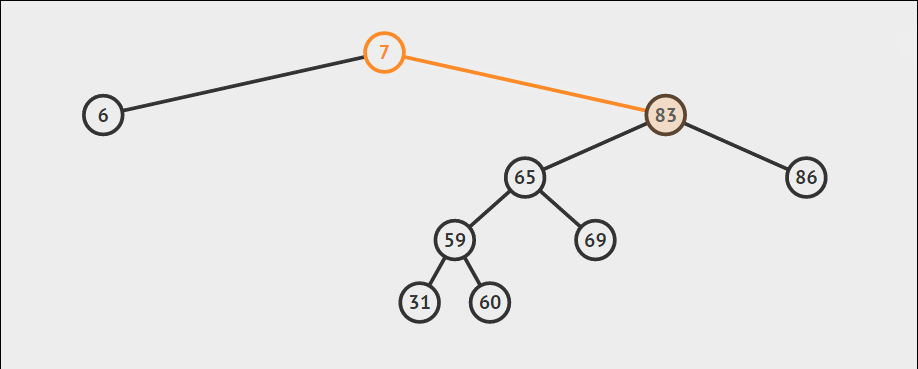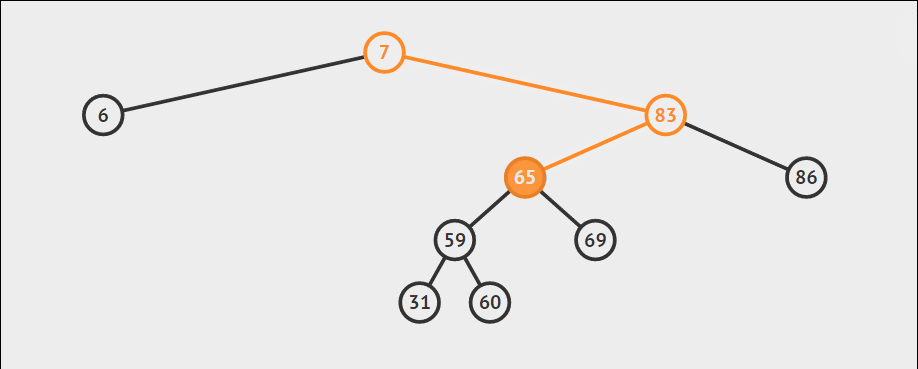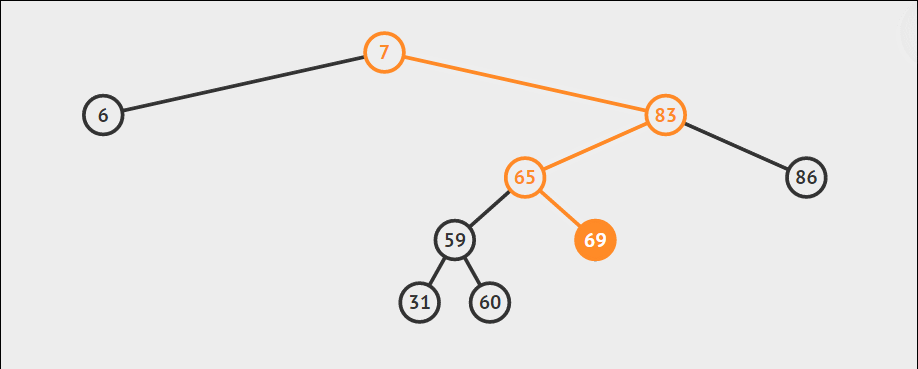上图为查找 69 的过程。
查找最大最小值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Position FindMin(SearchTree T)
{
if (T == NULL) {
return NULL;
}
else if (T->Left == NULL) {
return T;
}
else {
return FindMin(T->Left);
}
}
Position FindMax(SearchTree T)
{
if (T != NULL) {
while (T->Right != NULL) {
T = T->Right;
}
}
return T;
}
根据二叉搜索树性质，最大最小值必然分别出现在右下角和左下角，不断向右到底和向左到底即可完成。其中查找最小值利用递归实现，查找最大值利用循环实现。
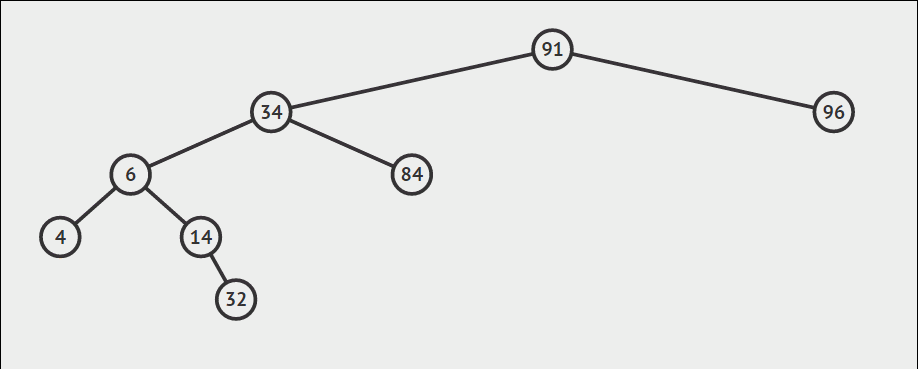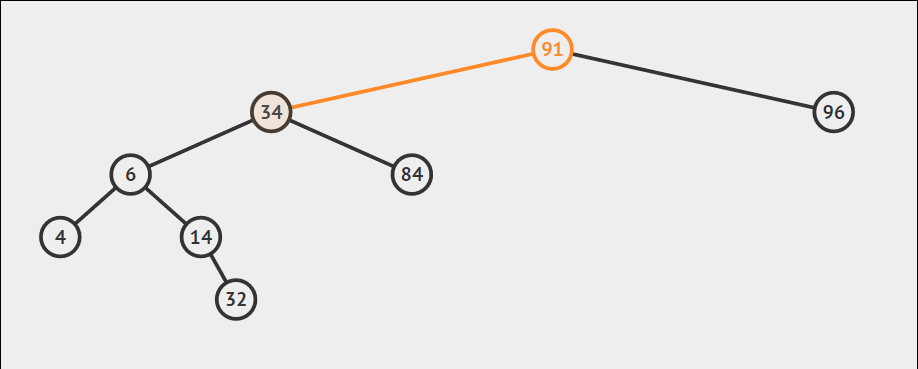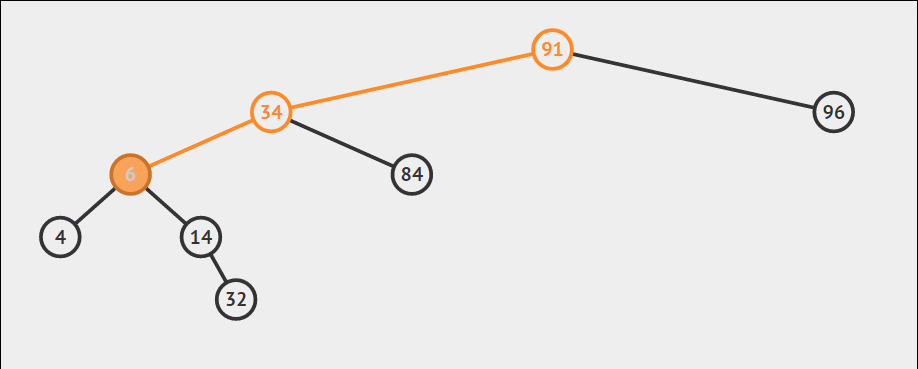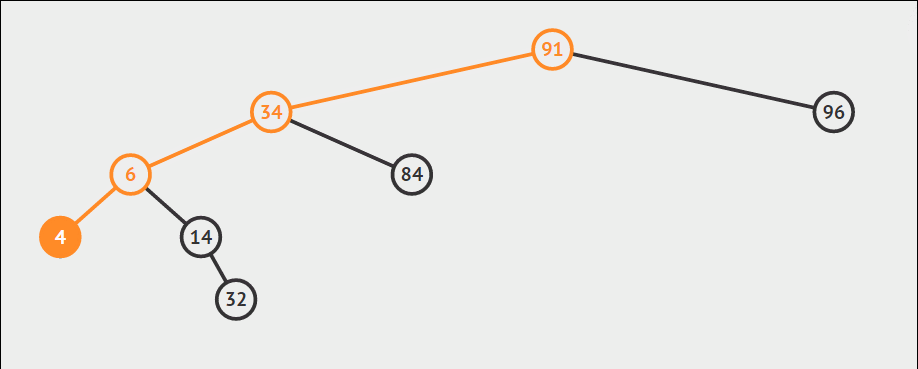
插入
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
SearchTree Insert(int x, SearchTree T)
{
if (T == NULL) {
T = (TreeNode* )malloc(sizeof(TreeNode));
T->data = x;
T->Left = NULL;
T->Right = NULL;
}
else if (x < T->data) {
T->Left = Insert(x, T->Left);
}
else if (x > T->data) {
T->Right = Insert(x, T->Right);
}
return T;
}
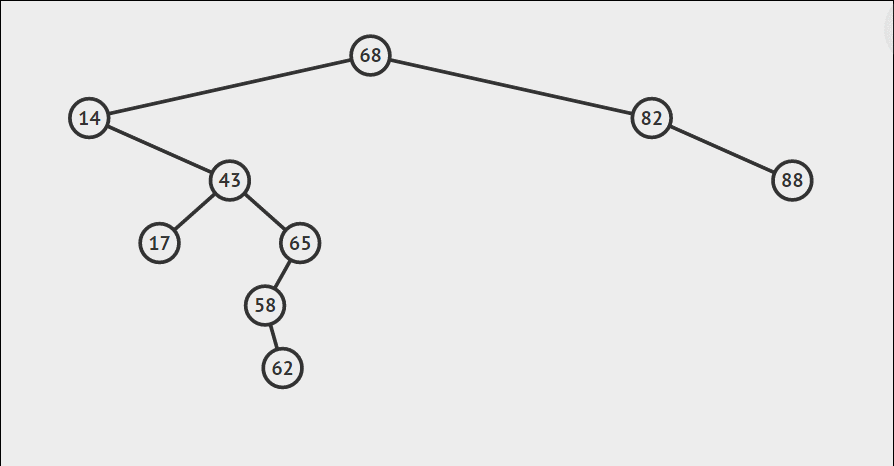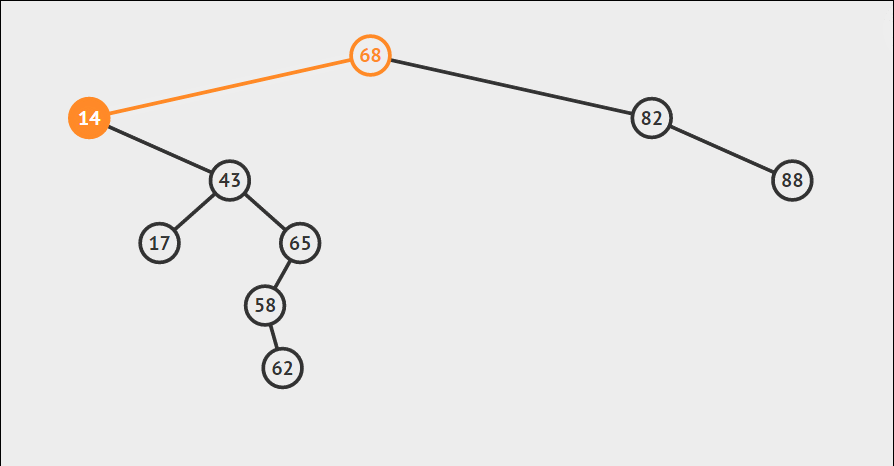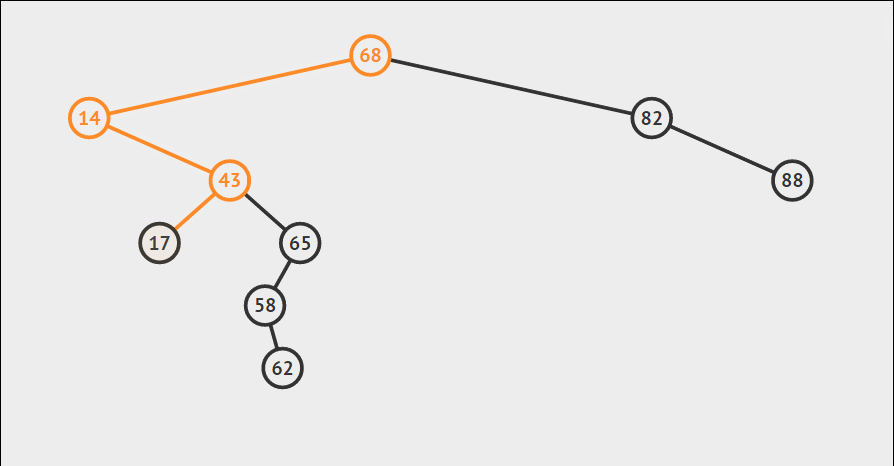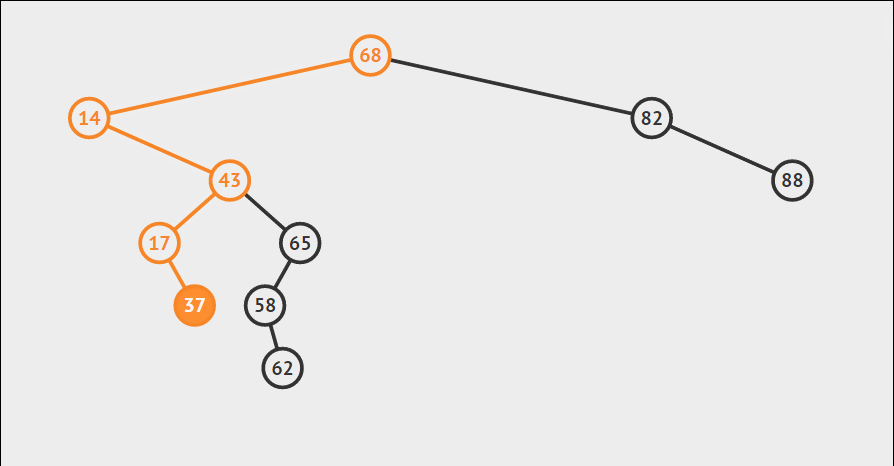
同样利用二叉搜索树性质，找到其所对应的父节点，然后当传入NULL的时候即代表这是所要插入的位置，返回新增节点地址，从而使得父节点可以指向新增节点，从而完成插入。
删除
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
SearchTree Delete(int x, SearchTree T)
{
Position Tmp;
if (x < T->data) {
T->Left=Delete(x, T->Left);
}
else if(x > T->data) {
T->Right=Delete(x, T->Right);
}//找到所要删除的节点
else
if (T->Left != NULL&&T->Right!= NULL) { //两个儿子的情况
Tmp = FindMin(T->Right);
T->data = Tmp->data;
T->Right = Delete(T->data, T->Right);
}
else { //一个或没有儿子的情况
Tmp = T;
if (T->Left == NULL) {
T = T->Right;
}
else if (T->Right == NULL) {
T = T->Left;
}
free(Tmp);
}
return T;
}
删除相对来说比较麻烦，因为涉及到两种不同的情况，首先依旧是利用递归找到要删除的节点位置，然后
-
一个或没有儿子。这种情况相对比较简单，只需要让其父节点直接指向该节点的儿子或者NULL，然后释放该节点即可。
-
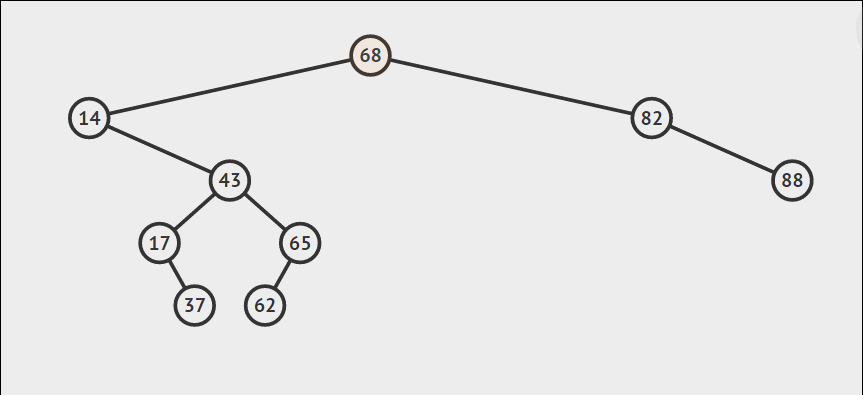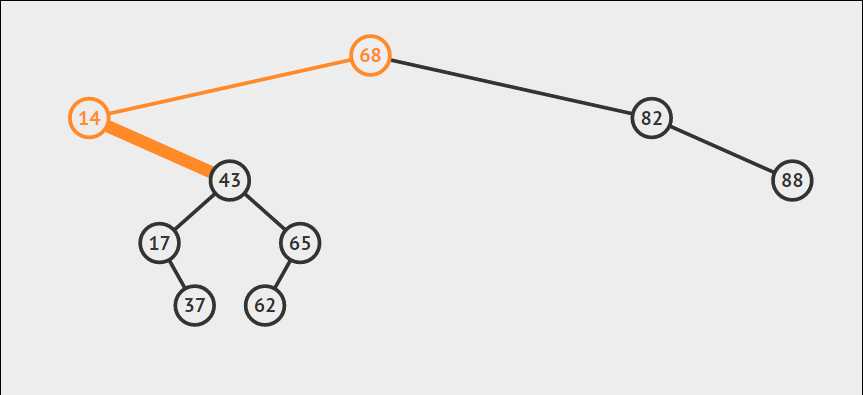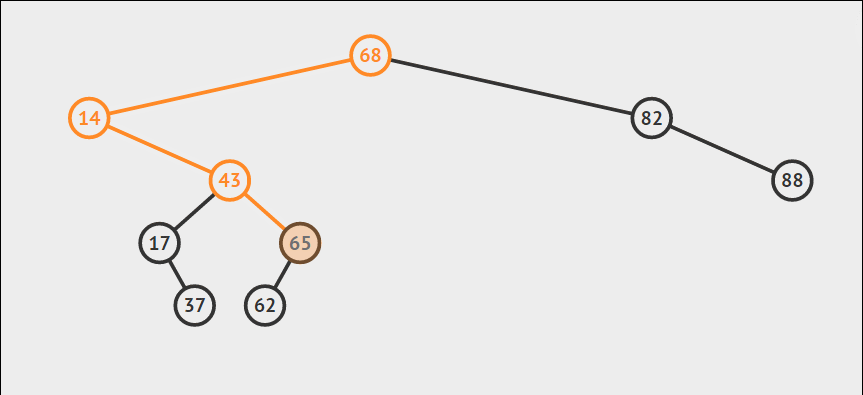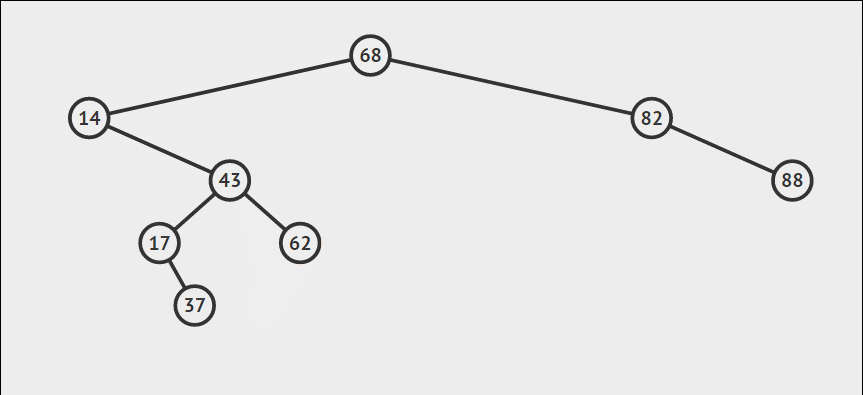
两个儿子。这种情况则比较复杂，普遍处理的方法为找到其右子树中最小的值替代要删除的节点位置的值，然后再递归删除右子树中最小的那个节点。而最小的节点通常在左下角的位置，属于第一种的简单情况，所以第二次删除相对比较容易。
图片和gif来自 visualgo.net
源代码均以上传至 GitHub